Trees

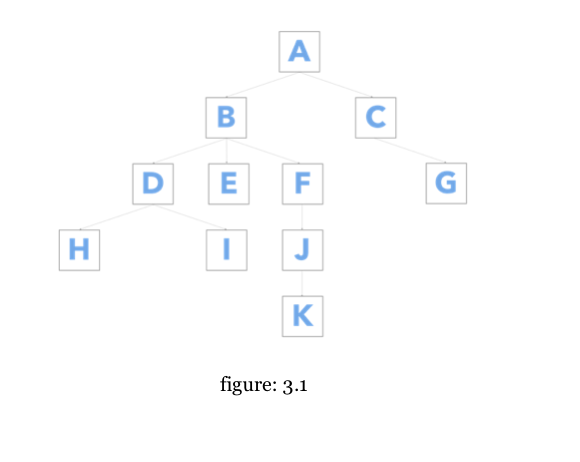
Binary Search Tree
in-Action with Alto.js
in-Action with Alto.js
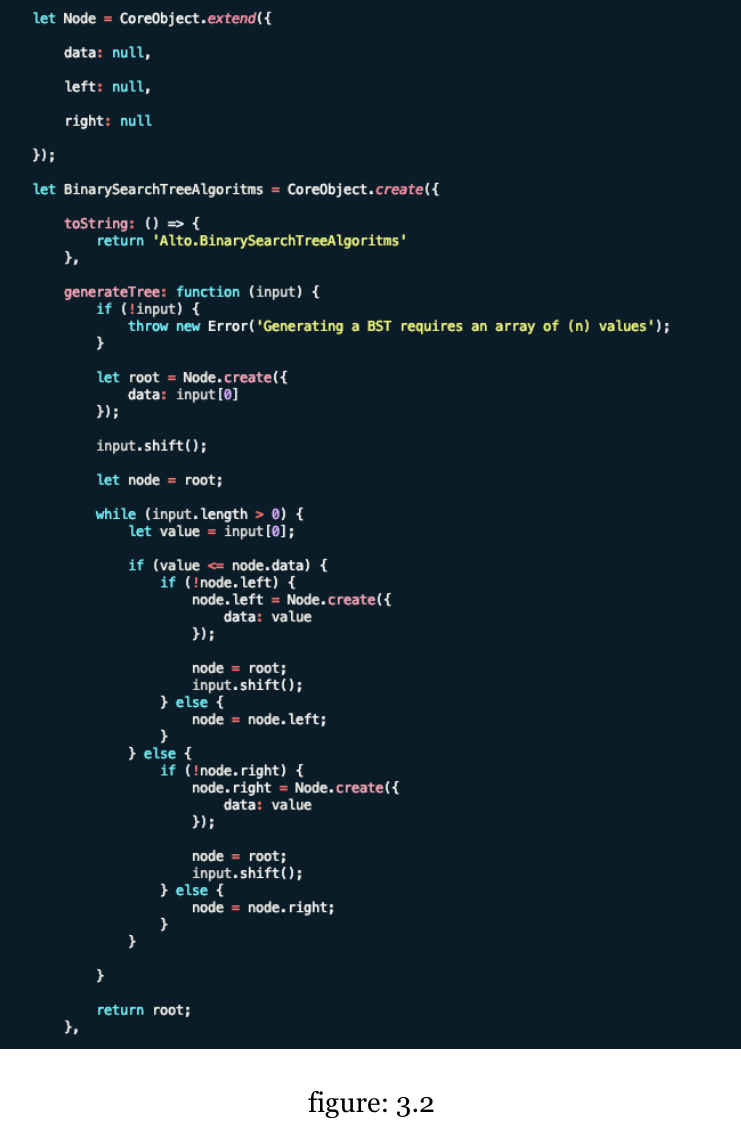
Depth First Traversals with Binary Search Tree:
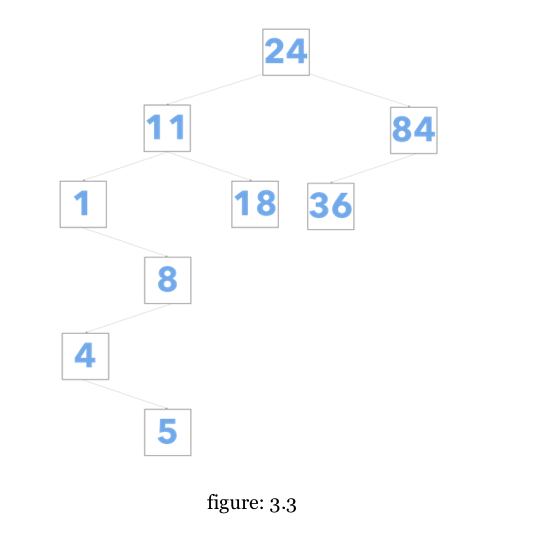
Preorder - Traverses a tree starting with the provided node, then all the left descendants and last all of the right descendants. Meaning, a node is always visited before any of its children. (self, left, right). Preorder traversal will visit our tree in figure 3.3 in the following order: (24, 11, 1, 8, 4, 5, 18, 84, 36)
Inorder - Traverses a tree starting with the provided node’s left descendants, then on the node itself, followed by the node’s right descendants. Meaning, the left subtree is visited first, then the node itself, and then the node’s right subtree. (left, self, right). Inorder traversal will visit our tree in figure 3.3 in the following order: (1, 4, 5, 8, 11, 18, 24, 36, 84)
Postorder - Traverses a tree starting with the provided node’s left descendants, then on the nodes right descendants, and finally on the node itself. Meaning, a node is always visited after its children. (left, right, self). Postorder traversal will visit our tree in figure 3.3 in the following order: (5, 4, 8, 1, 18, 11, 36, 84, 24)
Preorder - Traverses a tree starting with the provided node, then all the left descendants and last all of the right descendants. Meaning, a node is always visited before any of its children. (self, left, right). Preorder traversal will visit our tree in figure 3.3 in the following order: (24, 11, 1, 8, 4, 5, 18, 84, 36)
Inorder - Traverses a tree starting with the provided node’s left descendants, then on the node itself, followed by the node’s right descendants. Meaning, the left subtree is visited first, then the node itself, and then the node’s right subtree. (left, self, right). Inorder traversal will visit our tree in figure 3.3 in the following order: (1, 4, 5, 8, 11, 18, 24, 36, 84)
Postorder - Traverses a tree starting with the provided node’s left descendants, then on the nodes right descendants, and finally on the node itself. Meaning, a node is always visited after its children. (left, right, self). Postorder traversal will visit our tree in figure 3.3 in the following order: (5, 4, 8, 1, 18, 11, 36, 84, 24)
Preorder



Postorder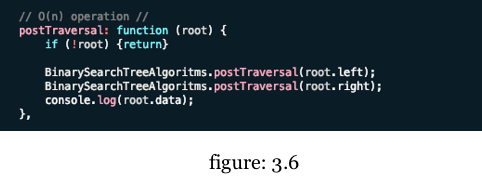

With our three depth first search algorithms explored, we can now perform other search actions on our binary search tree.
By modifying the logic of a preorder traversal, we can now find all leaves in our tree. When we visit “self” or the current node given, we check to see if the node has a left and right non-null data value. If true, then we found a leaf. Otherwise we call our findLeaves method again when there is a value for either node.left, node.right or both.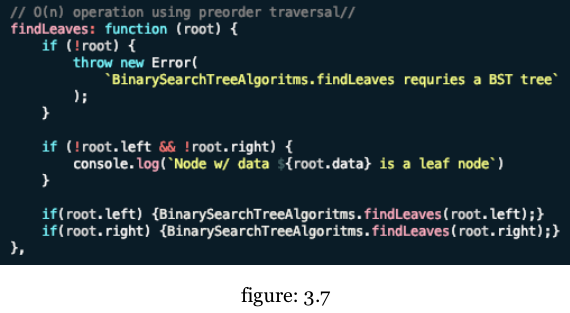
By modifying the logic of a preorder traversal, we can now find all leaves in our tree. When we visit “self” or the current node given, we check to see if the node has a left and right non-null data value. If true, then we found a leaf. Otherwise we call our findLeaves method again when there is a value for either node.left, node.right or both.


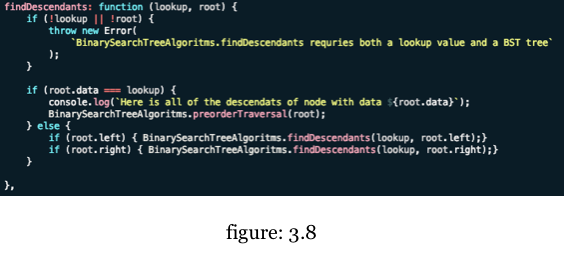
To find all ancestors of a given node. We check to see if the current nodes data is less than or greater than our lookup value. If it is less than, we move root to root.left and when it is greater than, we move out root to root.right. Before we move out root reference, we get the current value of root and push it into our ancestors array. When there is a match found, we return our ancestors.

Breadth First Traversal with Binary Search Tree:
A Breadth First Search is a bit more involved but once it is demystified its elegance is evident in its simplicity. BSF visits our tree in levels or rows.
On first traversal, we start with 24. On the next traversal we will be at level two. We visit level two in the following order, 11, 84. Then for the next traversal we will visit all of the level three nodes. Here 1, 18, 36 will be visited. And so forth.
To handle a breadth first traversal, we will need to use a queue and processed queue. Recursively visiting nodes, on the first traversal our queue will be [24] and the processed queue will be [24] as well. On the second traversal our queue will be [11, 84] and the processed queue will be [24, 11].
A Breadth First Search is a bit more involved but once it is demystified its elegance is evident in its simplicity. BSF visits our tree in levels or rows.
On first traversal, we start with 24. On the next traversal we will be at level two. We visit level two in the following order, 11, 84. Then for the next traversal we will visit all of the level three nodes. Here 1, 18, 36 will be visited. And so forth.
To handle a breadth first traversal, we will need to use a queue and processed queue. Recursively visiting nodes, on the first traversal our queue will be [24] and the processed queue will be [24] as well. On the second traversal our queue will be [11, 84] and the processed queue will be [24, 11].

